我试试用我的方式说说如何构造n维空间吧。

n维空间在n大于3后，说要画出来，有点难以想象。

但从数学的角度看，高维空间这个概念还算比较普通、容易理解的。

与其解释，不如快快开始。我选择用图(Graph)的方法来描述想说的东西，而且，我选的是特殊的某类空间，并且不是大多数人通常理解的空间。我选的空间的各个维度上只有一个比特——值只能在0和1之间取。数学符号表示是

下面会看到，这个模型会让人想到信息论里格雷码。但那是另一码事；我事实上忘了这种图论模型的名字，只是知道它而已。这里选择它，只是因为它的空间非常简单，我觉得应会比较容易感受维度的扩张如何进行。

首先希望大家放下对维度的先入之见。此处的维度，仅是 所说的自由度，并非大家通常理解的坐标轴的延伸方向。

开始吧。

首先是，

零维空间，没有维度——也即连一个可以取0-1值的比特都容不下。

但给它扩张一个维度后，

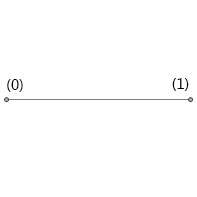就有点意思了。原先的一个点获得了一个方向分成了两头。此时图示对应的空间可以容纳一个取0-1值的比特，这个空间即成为一维的空间。

再扩张，

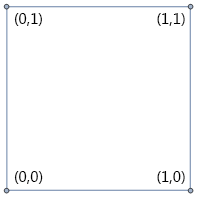这是空间可以容纳两个比特了，也即可以表示种状态。在该图里，开始可以看到维度是如何扩充的了：图的底下那条边，正是前一张图；将该条单边做一份拷贝，然后将原图和拷贝的两个顶点连接起来，就得到了这张图。

再按上述的方式扩张一次，

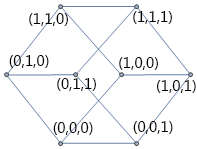此时，该图拥有了个顶点，可表示的状态也增长到这个数目；它所对应的空间扩张成了三维的，能容纳三个在0和1之间取值的比特。这里有个比较有趣的现象：

许多人倾向将这个图看作是立方体，哪怕他只是一个图(Graph)。

再来，应该是四维空间。大家可能都见过很多次的四维空间的标志物：

即这个问题的首页图：超立方体(Hypercube)。

事实上确实会得到超立方体，

（解释一下，首页图片上的这个图形也是两个立方体的八个顶点互相连接，只不过下面这个图是两个大小相同的立方体，而上面那个看起来一大一小）

如果你眼力比较好，可以看出这个图跟本问题的首页图是等价——妥妥的同一回事。该有的点都有，点和点之间该有的边都有，不该有的边都没有。这次的扩张，和前面的操作完全一样：

先取上一张图的原份，做一份拷贝；再将拷贝和原份的对应点连接起来，得到下一张图。

新图对应的空间，再次多了一个比特；同时能表示的状态翻了一倍。

上面各个过程，进行的操作是一样的：对空间的扩基(Extending basis)，将n-1维空间升级为n维空间。由数学归纳法，事实上我们可以得到任意维的空间。只是，我取的空间是特殊的。

但也不要认为这样的空间离欧氏空间很远——这种由比特组成的空间 (我忘了它的正式称谓) 的坐标值只能在两个离散值间取；假若各个坐标的取值都能取实数，那它就是欧氏空间

就介样，以后别说「画不出n维空间」这样的话了